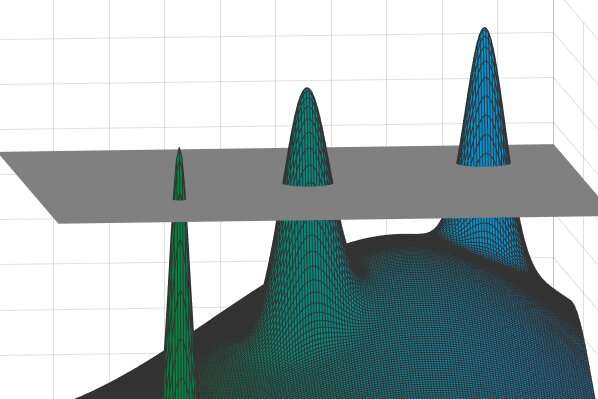
Σε ορισμένες περιπτώσεις, η διάμετρος κάθε κορυφής θα είναι πολύ μικρότερη από τις αποστάσεις μεταξύ των διαφορετικών κορυφών. Έτσι, αν κάποιος επέλεγε δύο σημεία σε αυτό το εκτεταμένο τοπίο -δηλαδή, δύο πιθανές “λύσεις” – θα ήταν είτε πολύ κοντά (αν προέρχονταν από την ίδια κορυφή) είτε πολύ μακριά (αν έλκονταν από διαφορετικές κορυφές) . Με άλλα λόγια, θα υπάρχει ένα ενδεικτικό «κενό» σε αυτές τις αποστάσεις – μικρό ή μεγάλο, αλλά τίποτα ενδιάμεσο. Πίστωση: David Jamarnik et al.
Η ιδέα ότι ορισμένα υπολογιστικά προβλήματα στα μαθηματικά και την επιστήμη των υπολογιστών μπορεί να είναι δύσκολα δεν πρέπει να προκαλεί έκπληξη. Υπάρχει, στην πραγματικότητα, μια ολόκληρη κατηγορία προβλημάτων για τα οποία θεωρείται αδύνατο να λυθούν μαθηματικά. Κάτω από αυτή την κατηγορία εμπίπτουν μερικά πιο «εύκολα» προβλήματα που δεν είναι καλά κατανοητά – και μπορεί επίσης να είναι αδύνατα.
Ο David Jamarnik, Καθηγητής Επιχειρησιακής Έρευνας στο MIT Sloan School of Management και στο Ινστιτούτο Δεδομένων, Συστημάτων και Κοινωνίας, εστιάζει την προσοχή του στην τελευταία κατηγορία των λιγότερο μελετημένων προβλημάτων, τα οποία είναι πιο σχετικά στον καθημερινό κόσμο, επειδή περιλαμβάνουν Τυχαίος— Βασικό χαρακτηριστικό των φυσικών συστημάτων. Αυτός και οι συνάδελφοί του έχουν αναπτύξει ένα ισχυρό εργαλείο για την ανάλυση αυτών των προβλημάτων που ονομάζεται ιδιότητα επικάλυψης κενού (ή OGP). Ο Gamarnik περιέγραψε τη νέα μεθοδολογία σε μια πρόσφατη ερευνητική εργασία στο Πρακτικά της Εθνικής Ακαδημίας Επιστημών.
P NP
Πριν από πενήντα χρόνια, διατυπώθηκε το πιο διάσημο πρόβλημα στη θεωρητική επιστήμη των υπολογιστών. P ≠ NP ρωτά, εάν υπάρχουν προβλήματα που αφορούν τεράστια σύνολα δεδομένων των οποίων η απάντηση μπορεί να επαληθευτεί σχετικά γρήγορα, αλλά τα οποία – ακόμα κι αν εργάζεστε στους ταχύτερους διαθέσιμους υπολογιστές – θα χρειαζόταν παράλογα πολύ χρόνο για να λυθούν.
Η εικασία P ≠ NP παραμένει αναπόδεικτη, ωστόσο οι περισσότεροι επιστήμονες υπολογιστών πιστεύουν ότι πολλά γνωστά προβλήματα – συμπεριλαμβανομένου, για παράδειγμα, του προβλήματος του ταξιδιώτη πωλητή – εμπίπτουν σε αυτήν την απίστευτα δύσκολη κατηγορία. Η πρόκληση στο παράδειγμα του πωλητή είναι να βρείτε τη συντομότερη διαδρομή, από άποψη απόστασης ή χρόνου, μέσω Ν διαφορετικών πόλεων. Η διαχείριση της εργασίας γίνεται εύκολα όταν N = 4, επειδή υπάρχουν μόνο έξι πιθανές διαδρομές που πρέπει να ληφθούν υπόψη. Αλλά σε 30 πόλεις, υπάρχουν περισσότερες από 1030 πιθανούς τρόπους, και οι αριθμοί αυξάνονται εκθετικά από εκεί. Η μεγαλύτερη δυσκολία έγκειται στο σχεδιασμό ενός αρχείου αλγόριθμος Λύνει το πρόβλημα γρήγορα σε όλες τις περιπτώσεις, για όλες τις ακέραιες τιμές του N., οι επιστήμονες υπολογιστών είναι βέβαιοι, βάσει της θεωρίας της υπολογιστικής πολυπλοκότητας, ότι δεν υπάρχει τέτοιος αλγόριθμος, επιβεβαιώνοντας ότι P ≠ NP.
Υπάρχουν πολλά άλλα παραδείγματα τέτοιων δυσεπίλυτων προβλημάτων. Ας υποθέσουμε, για παράδειγμα, ότι έχετε έναν τεράστιο πίνακα αριθμών με χιλιάδες σειρές και χιλιάδες στήλες. Μπορείτε να βρείτε, από όλους τους πιθανούς συνδυασμούς, την ακριβή διάταξη δέκα σειρών και 10 στηλών έτσι ώστε οι εκατό καταχωρήσεις τους να έχουν το υψηλότερο δυνατό άθροισμα; «Τις ονομάζουμε εργασίες βελτιστοποίησης, γιατί πάντα προσπαθείτε να βρείτε το μεγαλύτερο ή το καλύτερο — το μεγαλύτερο άθροισμα αριθμών, την καλύτερη διαδρομή μέσα από πόλεις κ.λπ.», λέει ο Jamarnik.
Οι επιστήμονες υπολογιστών έχουν από καιρό συνειδητοποιήσει ότι δεν μπορείτε να δημιουργήσετε έναν γρήγορο αλγόριθμο που μπορεί, σε όλες τις περιπτώσεις, να λύσει προβλήματα τόσο αποτελεσματικά όσο το έπος του περιοδεύοντος πωλητή. «Είναι πιθανό ότι κάτι τέτοιο θα ήταν αδύνατο για καλά κατανοητούς λόγους», σημειώνει ο Jamarnik. “Αλλά στην πραγματική ζωή, η φύση δεν δημιουργεί προβλήματα από εχθρική σκοπιά. Δεν προσπαθεί να σε απογοητεύσει με ένα λεπτώς επιλεγμένο, πιο απαιτητικό πρόβλημα που μπορεί να διανοηθεί.” Στην πραγματικότητα, οι άνθρωποι συνήθως αντιμετωπίζουν προβλήματα κάτω από πιο τυχαίες και λιγότερο διαχειριζόμενες συνθήκες, και αυτά είναι τα προβλήματα που στοχεύει να αντιμετωπίσει η εταιρική σχέση ανοιχτής κυβέρνησης.
Κορυφές και κοιλάδες
Για να κατανοήσετε τι είναι η εταιρική σχέση ανοιχτής διακυβέρνησης, ίσως είναι χρήσιμο να δούμε πρώτα πώς προέκυψε η ιδέα. Από τη δεκαετία του 1970, οι φυσικοί μελετούν το spin glass – υλικά που έχουν ιδιότητες τόσο υγρών όσο και στερεών που έχουν ασυνήθιστη μαγνητική συμπεριφορά. Η έρευνα στα περιστρεφόμενα ποτήρια οδήγησε σε μια γενική θεωρία περίπλοκων συστημάτων που σχετίζονται με προβλήματα στη φυσική, τα μαθηματικά, την επιστήμη των υπολογιστών, την επιστήμη των υλικών και άλλους τομείς. (Αυτό το έργο χάρισε στον Giorgio Baresi το Νόμπελ Φυσικής 2021.)
Ένα μπερδεμένο ζήτημα που έχουν αντιμετωπίσει οι φυσικοί είναι η προσπάθεια πρόβλεψης της ενεργειακής κατάστασης, ιδιαίτερα των χαμηλότερων ενεργειακών διαμορφώσεων, διαφορετικών δομών περιστρεφόμενου γυαλιού. Η κατάσταση μερικές φορές απεικονίζεται σε ένα «τοπίο» από αμέτρητες βουνοκορφές που χωρίζονται από κοιλάδες, όπου στόχος είναι να εντοπιστεί η ψηλότερη κορυφή. Σε αυτήν την περίπτωση, η υψηλότερη κορυφή αντιπροσωπεύει στην πραγματικότητα τη χαμηλότερη ενεργειακή κατάσταση (αν και θα μπορούσε κανείς να γυρίσει την εικόνα και να αναζητήσει τη βαθύτερη τρύπα). Αυτό αποδεικνύεται ότι είναι ένα πρόβλημα βελτιστοποίησης παρόμοιο σε μορφή με το δίλημμα του περιοδεύοντος πωλητή, ο Jamarnik εξηγεί: “Έχετε αυτό το τεράστιο σύνολο βουνών και φαίνεται ότι ο μόνος τρόπος για να βρείτε ψηλότερα είναι να σκαρφαλώσετε το καθένα”—μια παράλογη αγγαρεία παρόμοια να βρει μια βελόνα σε μια θημωνιά.
Οι φυσικοί έχουν δείξει ότι μπορείτε να απλοποιήσετε αυτήν την εικόνα και να κάνετε ένα βήμα προς μια λύση, κόβοντας βουνά σε ένα συγκεκριμένο προκαθορισμένο ύψος και αγνοώντας τα πάντα κάτω από αυτό το επίπεδο αποκοπής. Στη συνέχεια, θα αφήσετε μια ομάδα από εμφανείς κορυφές πάνω από ένα ομοιόμορφο στρώμα νεφών, με κάθε σημείο σε αυτές τις κορυφές να αντιπροσωπεύει μια πιθανή λύση στο αρχικό πρόβλημα.
Σε μια ερευνητική εργασία του 2014, ο Jamarnik και οι συνεργάτες του σημειώνουν κάτι που προηγουμένως αγνοούνταν. Συνειδητοποίησαν σε ορισμένες περιπτώσεις ότι η διάμετρος κάθε κορυφής θα ήταν πολύ μικρότερη από τις αποστάσεις μεταξύ των διαφορετικών κορυφών. Έτσι, εάν κάποιος επρόκειτο να επιλέξει οποιαδήποτε δύο σημεία σε αυτό το απέραντο τοπίο -δηλαδή δύο πιθανές “λύσεις” – θα ήταν είτε πολύ κοντά (αν προέρχονταν από την ίδια κορυφή) είτε πολύ μακριά (αν αντλούνταν από διαφορετικές κορυφές). Με άλλα λόγια, θα υπάρχει ένα ενδεικτικό «κενό» σε αυτές τις αποστάσεις – μικρό ή μεγάλο, αλλά τίποτα ενδιάμεσο. Ο Jamarnik και οι συνεργάτες του πρότειναν ότι το σύστημα σε αυτή την περίπτωση χαρακτηρίζεται από OGP.
“Βρήκαμε ότι όλα τα γνωστά προβλήματα υπολογιστικά δύσκολης τυχαίας φύσης έχουν μια εκδοχή αυτής της ιδιότητας” – δηλαδή, η διάμετρος του βουνού στο σχηματικό μοντέλο είναι πολύ μικρότερη από την απόσταση μεταξύ των βουνών, ισχυρίζεται ο Jamarnik. “Αυτό παρέχει μια πιο ακριβή μέτρηση της ευρωστίας του αλγορίθμου.”
Ξεκλείδωμα των μυστικών της πολυπλοκότητας του αλγορίθμου
Η έλευση του OGP θα μπορούσε να βοηθήσει τους ερευνητές να αξιολογήσουν τη δυσκολία δημιουργίας γρήγορων αλγορίθμων για την αντιμετώπιση συγκεκριμένων προβλημάτων. Τους έχει ήδη δώσει τη δυνατότητα να «μαθηματικά [and] Απέκλεισε κατηγορηματικά μια μεγάλη κατηγορία αλγορίθμων ως πιθανούς ανταγωνιστές», λέει ο Jamarnik. Μάθαμε, συγκεκριμένα, ότι οι σταθεροί αλγόριθμοι – αυτοί των οποίων η έξοδος δεν θα αλλάξει πολύ αν αλλάξει λίγο η είσοδος – θα αποτύχουν να λύσουν αυτού του είδους το πρόβλημα βελτιστοποίησης. «Αυτό το αρνητικό αποτέλεσμα ισχύει όχι μόνο για τους κλασσικούς υπολογιστές αλλά και για τους κβαντικούς υπολογιστές, και συγκεκριμένα, για τους λεγόμενους «αλγόριθμους βελτιστοποίησης κβαντικής προσέγγισης» (QAOAs), για τους οποίους ορισμένοι ερευνητές ήλπιζαν ότι θα έλυνε τα ίδια προβλήματα βελτιστοποίησης. Τώρα λαμβάνοντας υπόψη τα αποτελέσματα του Jamarnik και Σύμφωνα με τα ευρήματα των συν-συγγραφέων, αυτές οι ελπίδες μετριάζονται από την αναγνώριση ότι θα απαιτηθούν πολλά επίπεδα λειτουργιών για να επιτύχουν αλγόριθμοι τύπου QAOA, κάτι που μπορεί να είναι τεχνικά προκλητικό.
«Το αν πρόκειται για καλά ή κακά νέα εξαρτάται από την άποψή σας», λέει. “Πιστεύω ότι είναι καλά νέα με την έννοια ότι μας βοηθά να ξεκλειδώσουμε τα μυστικά της αλγοριθμικής πολυπλοκότητας και ενισχύουν τις γνώσεις μας για το τι υπάρχει στη σφαίρα των πιθανοτήτων και τι όχι. Είναι κακά νέα με την έννοια ότι μας λένε ότι αυτά τα προβλήματα είναι δύσκολα, ακόμα κι αν τα παράγει η φύση, και ακόμα κι αν παράγονται τυχαία». Προσθέτει ότι τα νέα δεν προκαλούν έκπληξη. «Πολλοί από εμάς το περιμέναμε όλο αυτό, αλλά τώρα έχουμε μια πολύ πιο σταθερή βάση για να κάνουμε αυτόν τον ισχυρισμό».
Αυτό εξακολουθεί να αφήνει τους ερευνητές έτη φωτός μακριά από το να μπορέσουν να αποδείξουν ότι δεν υπάρχουν γρήγοροι αλγόριθμοι που να μπορούν να λύσουν αυτά τα προβλήματα βελτιστοποίησης σε τυχαίες ρυθμίσεις. Η ύπαρξη τέτοιων στοιχείων θα έδινε μια οριστική απάντηση στο πρόβλημα P NP. Λέει, «Εάν μπορούμε να αποδείξουμε ότι δεν μπορούμε να έχουμε έναν αλγόριθμο που λειτουργεί τις περισσότερες φορές, αυτό μας λέει ότι σίγουρα δεν μπορούμε να έχουμε έναν αλγόριθμο που λειτουργεί συνεχώς».
Η πρόβλεψη του χρόνου που θα χρειαστεί για να λυθεί το πρόβλημα P NP φαίνεται να είναι ένα δυσεπίλυτο πρόβλημα από μόνο του. Πιθανότατα θα υπάρχουν πολλές κορυφές για αναρρίχηση και κοιλάδες για να διασχίσετε, προτού οι ερευνητές αποκτήσουν μια πιο ξεκάθαρη προοπτική της κατάστασης.
David Jamarnik, The Nested Gap Property: A Topological Barrier to Optimization Over Stochastic Structures, Πρακτικά της Εθνικής Ακαδημίας Επιστημών (2021). DOI: 10.1073/pnas.2108492118
Εισαγωγή του
Ινστιτούτο Τεχνολογίας της Μασαχουσέτης
το απόσπασμα: ο ερευνητής αναπτύσσει νέο εργαλείο για την κατανόηση δύσκολων και φαινομενικά δυσεπίλυτων υπολογιστικών προβλημάτων (2022, 10 Ιανουαρίου) Ανακτήθηκε στις 11 Ιανουαρίου 2022 από https://phys.org/news/2022-01-tool-hard-problems-intractable.html
Αυτό το έγγραφο υπόκειται σε πνευματικά δικαιώματα. Ανεξάρτητα από οποιαδήποτε δίκαιη συναλλαγή για σκοπούς ιδιωτικής μελέτης ή έρευνας, κανένα μέρος δεν επιτρέπεται να αναπαραχθεί χωρίς γραπτή άδεια. Το περιεχόμενο παρέχεται μόνο για ενημερωτικούς σκοπούς.

“Ερασιτέχνης διοργανωτής. Εξαιρετικά ταπεινός web maven. Ειδικός κοινωνικών μέσων Wannabe. Δημιουργός. Thinker.”
