
Οι ερευνητές έχουν κάνει σημαντική πρόοδο στη φασματοσκοπική γεωμετρία αποδεικνύοντας μια ειδική περίπτωση της εικασίας του Bolya σχετικά με τις ιδιοτιμές του δίσκου. Το έργο τους, το οποίο συνδυάζει τη θεωρητική κομψότητα με πιθανές πρακτικές εφαρμογές, αναδεικνύει την παγκόσμια αξία και την καλλιτεχνική ομορφιά της μαθηματικής έρευνας. Πίστωση: SciTechDaily.com
Ένας καθηγητής και οι συνεργάτες του απέδειξαν την εικασία του Polya για τις ιδιοτιμές του δίσκου, ένα δύσκολο πρόβλημα στα μαθηματικά.
Μπορεί να συναχθεί το σχήμα του τυμπάνου από τους ήχους που κάνει;
Αυτό είναι το είδος της ερώτησης που αρέσκεται να κάνει ο Ιωσήφ Πόλτροβιτς, καθηγητής στο Τμήμα Μαθηματικών και Στατιστικής στο Πανεπιστήμιο του Μόντρεαλ. Ο Poltrovic χρησιμοποιεί τη φασματοσκοπική γεωμετρία, έναν κλάδο των μαθηματικών, για να κατανοήσει φυσικά φαινόμενα που περιλαμβάνουν τη διάδοση των κυμάτων.
Μια σημαντική ανακάλυψη στη μαθηματική εκτίμηση
Το περασμένο καλοκαίρι, ο Poltovic και οι διεθνείς συνεργάτες του – Nikolai Filonov, Michael Levitin και David Scherr – απέδειξαν μια ειδική περίπτωση της περίφημης εικασίας φασματοσκοπικής γεωμετρίας που διατυπώθηκε το 1954 από τον διαπρεπή Ουγγροαμερικανό μαθηματικό George Polya.
Η εκτίμηση αφορά την εκτίμηση των συχνοτήτων του στρογγυλού κυλίνδρου ή, με μαθηματικούς όρους, των ιδιοτιμών του δίσκου.
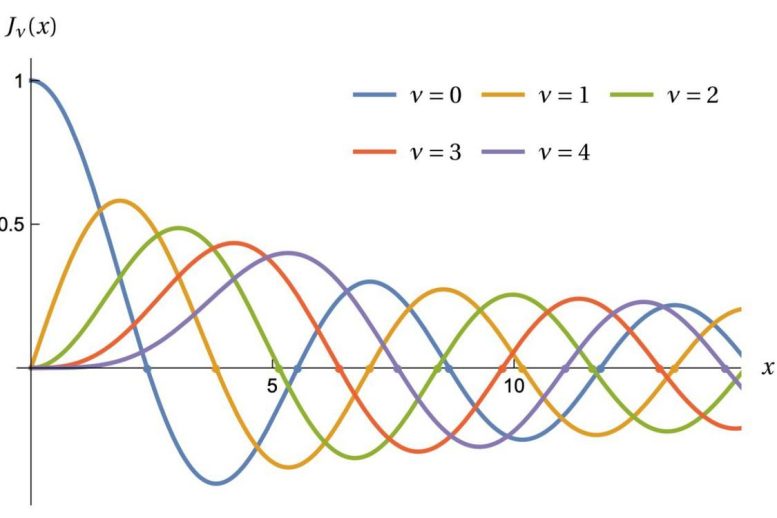
Αυτό το διάγραμμα δείχνει συναρτήσεις Bessel, όπου οι τελείες αντιστοιχούν στις συχνότητες των ήχων που παράγονται από ένα στρογγυλό τύμπανο. Πραγματοποίηση: Michael Levitin
Ο ίδιος ο Polya επιβεβαίωσε την εικασία του το 1961 σχετικά με τις σφαίρες που απαρτίζουν το επίπεδο, όπως τρίγωνα και ορθογώνια. Μέχρι πέρυσι, η εικασία ήταν γνωστή μόνο για αυτές τις περιπτώσεις. Ο δίσκος, παρά τη φαινομενική του απλότητα, παρέμεινε άπιαστος.
«Φανταστείτε ένα άπειρο πάτωμα καλυμμένο με πλακάκια του ίδιου σχήματος που ταιριάζουν μεταξύ τους για να γεμίσουν τον χώρο», είπε ο Poltovic. «Μπορούν να πλακωθούν με τετράγωνα ή τρίγωνα, αλλά όχι με δίσκους. Οι δίσκοι στην πραγματικότητα δεν είναι καλό σχήμα για πλακάκια.
Η καθολικότητα και η επίδραση των μαθηματικών
Σε άρθρο που δημοσιεύτηκε τον Ιούλιο του 2023 στο αθλητικό περιοδικό Μαθηματικές εφευρέσειςΟι ερευνητές έδειξαν ότι η εικασία του Bolya είναι σωστή για έναν δίσκο, μια περίπτωση που θεωρείται ιδιαίτερα δύσκολη.
Αν και τα αποτελέσματά τους είναι κυρίως θεωρητικής αξίας, η αποδεικτική τους μέθοδος έχει εφαρμογές στα υπολογιστικά μαθηματικά και στους αριθμητικούς υπολογισμούς. Οι συγγραφείς διερευνούν τώρα αυτήν την προσέγγιση.

Τζόζεφ Πόλτροβιτς
«Παρόλο που τα μαθηματικά είναι μια βασική επιστήμη, μοιάζουν με τον αθλητισμό και τις τέχνες κατά κάποιο τρόπο», είπε ο Πόλτροβιτς.
“Το να προσπαθείς να αποδείξεις μια μακροχρόνια εικασία είναι ένα άθλημα. Η εύρεση μιας κομψής λύσης είναι τέχνη. Σε πολλές περιπτώσεις, οι όμορφες μαθηματικές ανακαλύψεις είναι χρήσιμες, απλά πρέπει να βρεις τη σωστή εφαρμογή.”
Αναφορά: «The Polya Conjecture for Euclidean Spheres» των Nikolai Filonov, Michael Levitin, Iosif Poltovic και David A. Κοινοποίηση, 5 Ιουνίου 2023, Μαθηματικές εφευρέσεις.
doi: 10.1007/s00222-023-01198-1

“Ερασιτέχνης διοργανωτής. Εξαιρετικά ταπεινός web maven. Ειδικός κοινωνικών μέσων Wannabe. Δημιουργός. Thinker.”


